Growth rate of the GDP per capita revisited. 1. Comparison of the TED 2013 and Maddison Project Database 2020

The history of physics has many examples when the measured values of fundamental physical constants were corrected according to new measurements using more sensitive instruments and methods. A good example is a change in the gravitational constant. In economics, the changing time series is commonplace. Moreover, most of the economic time series are accompanied by disclaimers that the measurements in adjacent years are incompatible due to change in measurement methodology and/definition of parameters. This is true even for such a simple process as population counting, and the population estimates are corrected many times back in the past. That's why I admire people who spend enormous efforts and time to correct economic time series and provide an unbiased set of economic parameters for all measurable economies.  Here, I would like to express my admiration to Angus Maddison and his excellent team, they continued this extremely important study after Angus passed away in 2010.  I hope that any study with the data borrowed from the Maddison Project Database (MPD) is an expression of deep respect and trust to the quality of the MPD data. The MPD  was the Total Economy Database (TED) of the Conference Board before it was renamed in 2016.

In many previous posts in this blog (e.g., 1, 2, 3), in a number of papers [1, 2, 3] and a book, we presented an extensive analysis of the linear growth in the GDP per capita (GDPpc)  in developed countries. This analysis was based on the GDPpc time series from the Total Economy Database and, in some cases,  covered the time period since the 19th century as allowed by the TED data. Here, we have to return to the first paragraph and to estimate the changes in the MPD time series relative to the 2013 TED, which was used in our previous publications. This is a mandatory methodological step in any study based on alternating data, e.g. the difference between the 2010 and 2013 TEDs is dramatic for some countries.

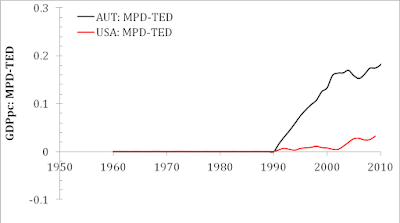
Figure 1 presents the evolution of the GDPpc in the USA and Austria and compares the 2013 TED and 2020 MPD. The relative values are needed, i.e. all 4 time series are normalized their respective levels in 1960,  since the reference year in the chained dollar time-series changes with new editions. Both time series for the USA is practically identical with very low-amplitude deviations since 1990 (total growth since 1960 is 2.65 for the TED 2013 and 2.68 for the MPD, i.e. (2.65-2.68)/2.68 =0.9988 or -1.1% ), as Figure 2 shows, where the difference between the MPD 2020 and TED 2013 is depicted. For Austria, the difference since 1990 has a larger amplitude, and the overall growth in the GDPpc since 1960 is 3.82 in the TEB 2013 and 4.00 for the MPD, i.e. 4.4%. In absolute values, the difference in the total growth is 0.03 units in the USA and 0.18 units in Austria. Therefore, the GDPpc evolution in Austria has important updates in the MPD, which may result in not negligible differences in the estimation of growth rates. 

In a series of future posts, we are going to revisit our previous estimates of the GDPpc growth (and the accuracy of the corresponding model) in developed countries and  some countries with data available in the OECD database.  It is important to use data from the same source for all countries in order to avoid the bias introduced by definitions and estimation procedures. The MPD has data on GDPpc and total population, but has no times series for the working-age population, which we use to correct the GDPpc data for the difference between total and economically active (with income) population. Therefore, we have to use the OECD data on population age pyramid, and thus, to limit the set of studied countries. Another constraint from the OECD is that the population time series starts in 1960 and we use the time interval between 1960 and 2018 (the last year with data in the MPD). The choice of this time interval might guarantee a more accurate estimation since the period of the dramatic and turbulent change in GDPpc trend covers the years between 1940 and 1950, but some aftermaths of such a turbulent change might be observed a few years after 1950. In any case, we are going to check if the MPD 2020 has significant differences with the TED 2013 for all studied countries and to report such differences in case they introduce game-changing disturbances.

Figure 1. Comparison of the MPD and TED(2013) GDPpc time series for Austria (AUT) and the USA. The GDPpc evolution in Austria has important updates in the MPD, which may result in not negligible differences in the estimation of growth rates.   

Figure 2. The difference between the MPD 2020 and TED 2013 presented in Figure 1. For Austria, the difference in 2012 was 0.18 units of GDPpc total growth. This is a significant change in the time series.