Economics as Classical Mechanics: Time to validate economic models: data quality analysis for the relationship between unemployment and real GDP

The driving forces behind the change in unemployment (rate) in developed economies represent a very important and actual problem for the modern economic theory. For example, there exists an opinion that the change in unemployment may manifest tangible structural changes in the labor market. The COVID-19 pandemic is a natural non-economic (exogenous forces) experiment to test and validate all economic theories of unemployment. One can expect major changes in the overall organization of all economies (developed, emerging, etc.) when significant parts of them are suppressed or just decimated due to non-economic reasons. In this blog, we addressed the problem of structural unemployment by modeling the rate of unemployment with Okun’s law, i.e. the relationship of unemployment and real GDP growth.

The COVID-19 pandemic is a deciding/survival opportunity for any quantitative economic theory like Okun’s law. Obviously, all descriptive economic theories never take data seriously, and these religious sects have their own apologists and believers: “In the beginning was the Word”. In a series of future posts, we are going to revisit and validate our previous results obtained for a specific version of Okun’s law developed in a series of papers. The last overview of our empirically estimated Okun-style models for selected developed countries (the United States, France, the United Kingdom, Australia, Canada, and Spain) was published in 2011. The quantitative results suggest the absence of structural unemployment in the studied developed countries. The persistence of high unemployment is completely related to a low rate of real economic growth.

This overview used the data between 1950 and 2009 from two principal sources – the Total Economy Database of the Conference Board and the OECD. Currently, the data on real GDP per capita and unemployment are available for the years between 2010 and 2019. We use the same data sources (Maddison Project Database instead of the TED) and compare the selected time series with similar time series from the BEA and BLS.

In our previous work, we had to introduce (virtual) structural breaks in Okun’s law in order to improve the agreement between the change in the unemployment rate and real GDP per capita. As we described in several posts in December 2020, such breaks likely manifest artificial changes in definitions of unemployment and real GDP rather than actual shifts in the economic behavior of the variables in Okun’s law. The crucial importance of data quality and consistency for quantitative analysis makes is mandatory to check all time series of unemployment, employment, labor force, and real GDP per capita for definitional breaks and also to compare similar time series from different sources. Any deviation between similar time series from different sources should be considered as an estimate of measurement accuracy and resolution.

To begin with, we compare the CPI and GDP deflator (dGDP) in the USA since 1929. The deviation between these two price inflation estimates as discussed in details (post2011, post2020) and here we would like to highlight the change in coefficients needed to match the CPI and dGDP curves. Also, we include the Personal Consumer Expenditure (PCE) index in the discussion. The PCE is a major component of the Gross Domestic Product. Figure 1 presents all three indices in panel a), where the corresponding time series are normalized to their respective values in 1929, i.e. 1929 is the reference year. The (total price increase) CPI curve starts to deviate from the PCE and dGDP curves since the late 1970s. The PCE and dGDP curves are very close in their cumulative representation. Panel b) in Figure 1, depicts the cumulative inflation, i.e. the sum of annual inflation rates, for the three indices. This representation is more sensitive to the differences in the indices and one can observe slight deviations between the PCE and dGDP, as well as the discrepancy between the PCE and dGDP in the late 1940s.

Figure 1. a) The price increase as described by the CPI, PCE, and GDP deflator in the USA since 1929. All curves are reduced to their respective levels in 1929. Data are borrowed from the BEA and BLS. The CPI price increase becomes higher than the PCE and GDP price growth since 1979. b): The cumulative inflation (i.e. the sum on annual inflation readings in percentage points) according to price indices: CPI, PCE, and GDP deflator. Deviations between the three curves are better seen in this representation.

Figure 2 depicts the differences between the annual inflation estimates and the cumulative inflation curves for all three pairs of the studied indices. Panel a) shows the CPI and dGDP differences. The difference between the cumulative inflation curves reveals the deviation between these two approaches to price inflation. Before 1978, the difference between the CPI and dGDP curves was hovering in the range between -5 and +5. It looks like that the CPI was the basis of the GDP deflator. The period between 1981 and 2001 could be well approximated by a linear function. The years between 1978 and 1980 are like a spike or a correction distributed over 3 years. As we know, there was a comprehensive NIPA (national income and product accounts) revision around 1980 and the effect of this revision was distributed over years. It is not excluded that the comprehensive NIPA revisions may include new elements making the real GDP time series incompatible in time.

Since we were limited to 2009 in our previous study in 2011, the segment between 2010 and 2019 is of the largest interest for the model validation. It is important to stress that there was a comprehensive NIPA revision in 2010. For Okun’s law, these revisions mean the change in the coefficients of linear regression between the GDP per capita and the rate of unemployment, i.e. virtual breaks in the dependence one can confuse with structural breaks in economic behavior. One can also pretend that the years between 2001 revision and 2010 revision to the GDP definition are characterized by a slightly lower slope of the different line than the years between 1982 and 2000. Potentially, there should be a break in 2001, but it might be too small to affect statistical estimates of our model.

Panel b) in Figure 2 presents the same curves for the CPI-PCE pair. The PCE is close to the dGDP and the general features of the difference between cumulative inflation curves are similar to those in panel a). In panel c), the differences for the dGDP-PCE pair are presented. One can see that the dGDP and PCE indexes are slightly different. Interestingly, the level of variation in the differences between the CPI and PCE cumulative curves is higher before 1990 than after 1990. This observation is likely related to the improvement in the definition.

Figure 2. a) The difference of the annual and cumulative inflation estimates for the CPI and GDP deflator in the USA since 1929. b): The difference of the annual and cumulative inflation estimates for the CPI and the PCE in the USA since 1929.

Figure 3 demonstrates that the PCE gives from 59% to 68% of the real GDP. Panel c) in Figure 3 is likely the most important for the success of the current study - it shows the change in various real GDP components in 2020. The quarter-to-quarter change rate in real GDP in the second quarter of 2020 was -36% and +30% in the third quarter. The PCE dropped by 38.0% in the second quarter and increase by 36% in the third.

According to our version of Okun’s law, the fall in real GDP per capita results in an increase in the rate of unemployment. The linear regression coefficient for the period before 2010 was -0.465 and the constant term was 0.9. When applied to the fall in the real GDP per capita these coefficients would give 21% unemployment rate in the second quarter. (Here we have to use the real GDPpc instead of real GDP.) The observed rate was 13.3%. The discrepancy is probably due to the break in the regression coefficients in 2010. To match the unemployment rate observed in the second quarter of 2020, the model needs the regression coefficient has to be ~0.25. The years between 2010 and 2019 have to be used to estimate the regression coefficient after the 2010 break. The recovery in the third quarter is also an important observation for the model validation.

Figure 3. a) Components of the GDP. Personal Consumer Expenditures (PCE) varies between 59% and 68%. b) Contributions to Percent Change in Real Gross Domestic Product. c) The quarterly rate of change in real GDP components.

In Figure 4, the GDP deflator is split into its major components and the total price change (panel a) and inflation rates (panel b) are presented. In panel c) we show the quarterly (y/y) estimates of the price inflation rates. In 2020, only exports and imports demonstrate a negative inflation rate. The dGDP and PCE inflation rates are positive (0.6%). We are going to use the dGDP and PCE price inflation estimates in the extended model linking inflation, unemployment, and labor force. The accuracy of inflation estimates is crucial for this model.

Figure 4. a) The evolution of the GDP price deflator and its components since 1929. The GDP deflator is very close to the PCE, as the largest input to the GDP. b) Price inflation of the components in panel a). The largest inflation is related to Imports. c) Quarterly (y/y) inflation estimates for the GDP major components. Imports and exports demonstrate the largest fall in 2020.

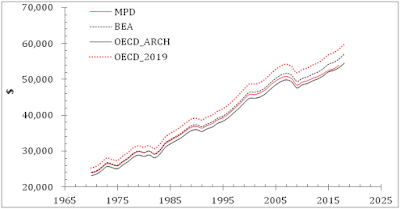
Finally, the real GDP per capita estimates may differ between the major providers of economic data. Figure 5 presents four different real GDP per capita curves for the USA: the Maddison Project Database, Bureau of Economic Analysis, and two curves from the OECD. Because of varying reference years and corresponding reference real GDPpc levels, the curves are similar is shape but have different levels. In the lower panel of Figure 5, the change rates (y/y) are presented and the difference between them is most prominent after 2010. The period between 2010 and 2020 is characterized by the highest uncertainty in GDP per capita.

Figure 6 depicts the ratio of the MPD GDP per capita and three other time series, all 4 series are first normalized to their respective levels in 1970 and the ratios are calculated. As a result, all ratios start from 1 and one can see the discrepancy of the real GDP per capita estimates. For example, the MPD/BEA curve drops to 0.98 in 2015, and the other two ratios fall even deeper to 0.975. In standard statistical analysis, the results may differ, especially after 2010. Figure 7 illustrates the change in the real GDPpc estimates published by the same agency - OECD. One cannot exclude the possibility that the current estimates of any economic parameters are subject to revisions in the future, and these revisions may change statistical estimates for all economic relationships.

Figure 5. Upper panel: Four real GDP per capita curves reported by different economic agencies. Lower panel: the reported change rates are slightly different between the agencies.