Income inequality: race and gender issues

(Outline of  future paper - no references and equations)

Introduction

Here we analyse the evolution of two specific features of gender dependent personal income for three races in U.S. population: white, black and Hispanic. Our analysis includes extensive processing of actual data and theoretical consideration at the microeconomic level. In contrast to all other studies of income inequality we quantitatively predict individual incomes in a given economy together with various aggregate measures (e.g. the Gini ratio) using a complete dynamic model. This is an evolutionary model where the change of incomes is driven by one exogenous variable – real GDP per capita (for working age population) or mean personal income. This model allows to accurately describing all observed characteristics of personal income distribution. In this study, we explain the evolution of two age dependent parameters for various race/gender configurations. These two parameters are the mean income and the share of population in the Pareto distribution in the U.S. Both parameters are sensitive to gender/race configuration and their evolution is driven by real GDP per capita.

The evolution of age-dependent mean income demonstrates the overall lag between income earned by people of different gender and race, which cannot be surmounted without dramatic changes to the root social relationships between races and genders. The second feature highlights deep discrepancy in the proportion of people of different race and gender with the highest incomes (above $100,000). This disproportion is especially high for the youngest and eldest age categories.  The lack of presence in the high-income range makes the shape of the age-dependent mean income distribution for all “not-white-male” groups to lag by decades behind the white-male population. Our microeconomic model of personal income distribution and evolution reveals the fact that the observed disproportion in gender and race representation in the high-income range has a measurable negative impact on real economic growth in the U.S., not saying about the extremely high level of unjustified social disparity.

Overall behaviour and model

We start with a simple graph comparing trajectories of mean income for two genders and two races – white and black. Figure 1 also displays the mean personal income for all population as reported by the Census Bureau. Since white population prevails in the U.S. race structure the mean incomes for all male and female are close to those for the white. The advantage of white male over any other race and gender is obvious. The black male group is marginally above the white female one. The dominance of white male, as expressed by mean income, is obvious. Is it fair? In this study we give a negative answer to this question investigating the age-dependent mean income and the proportion of a given race-gender group in the high-income range (above $100,000).

Following the whole bulk of observations of personal income in the USA as well as in some other developed countries, our microeconomic model (here, we skip all technical details) links the change in any personal income and thus in the mean income shape with the only parameter – the level of real mean income as reported by the CB, which is shown by dotted black line in Figure 1. As a substitute, one can use real GDP per capita calculated for working age population. Mathematically, the work experience (i.e. the age of person less 15 years) for the peak mean income is proportional to the square root of real GDP per capita. For the change in real mean income from 1967 to 2013, the predicted age of peak mean income should increase from 44 to 53 years. Figure 4 compares the observed curve of mean income dependence on age for 1998 and that predicted by the microeconomic model. The overall shape and the age of peak income are predicted with striking accuracy.

Figure 1. The evolution of gender and race (white and black) dependent mean income as reported by the Census Bureau (CB) in constant 2013 U.S. dollars. White population prevails in the U.S. race structure and thus the mean incomes for all male and female are close to those for the white population. 

It is worth noting that the increasing duration of growth to peak value explains the problems with income in the youngest age group. The share of youngsters in total personal income falls with time and this is one of fundamental features of the US (as well as other developed countries) social structure.  This is an intrinsic feature of any developed economy (report on some other countries is under preparation). Larger real GDP per capita implies longer way for an average person to her/his peak income and thus a slower start for the youngest population. Figure 5 demonstrates that this feature of real income behaviour is also extremely well predicted by our model. We present two actual curves of mean income for 1962 and 2012 in the range from 15 to 28 years of age as estimated from the microeconomic data obtained from the IPUMS. The difference between these curves suggests that economic conditions for the youngest population have been deteriorating. In 1962, the mean income for 28-year-olds was around 80% of the peak mean income. In 2012, this level dropped to 60%. Two predicted curves shown by red and black lines, respectively, demonstrate the accuracy of model predictions. This allows us to predict that the conditions for the youngest population will be further deteriorating as a consequence of real economic growth. The model predicts exactly what will happen in the future with personal incomes depending on real GDP per capita. Time does not matter per ce – it is just a parameter to quantify real GDP estimates. It is worth noting that the best fit model year for actual 1962 data is obtained for the year of 1958. Considering the decreasing level of accuracy of GDP and mean income estimates in the past, this difference is just marginal.

For the level of measurement accuracy of the overall personal income distribution, the model predicts the increase in the peak age quite well. Our model is extensively used in fine data analysis and accurate predictions.  The US society is not a homogeneous one and genders and races demonstrate different features and long-term behaviour.  In the next paragraph, we consider some differences between races and genders.

Figure 2. The evolution of age-dependent nominal mean income between 1967 and 2013. 

Figure 3. The evolution of age-dependent mean income between 1967 and 2013.  Both curves in Figure 2 were smoothed with an eight-year-moving-average and then normalized to their respective peak values.

Figure 4. Comparison of the observed mean (averaged in five-year bins except the bin between 15 and 24 years of age) income dependence on work experience (open circles) and that predicted by our model (dotted line) for 1998. The model provides annual estimates. The age of peak mean income is accurately predicted as well as the shape of the observed curve. Our model describes the whole period between 1929 (start of the GDP time series in the U.S.) and 2013.

Figure 5. The evolution of mean income in the youngest age group. The actual mean income estimates for 1962 (red circles) and 2012 (black circles) are estimated from microeconomic data obtained from the IPUMS. The model predictions are shown by red and black lines, respectively. The best fit model year for actual 1962 data is obtained for the year of 1958. Considering the decreasing level of accuracy of GDP and mean income estimates in the past, this difference is just a marginal one.  

Race and gender: unfairness of income distribution

Figure 6 repeats Figures 2 and 3 for the mean income of white male population. Here we use the income values averaged in ten-year-wide bins (e.g., from 15 to 24 years of age) as reported by the CB. The curves for white males have the same striking feature as observed in the overall income distribution – the increase in the age of mean income peak. Figure 7 supports this observation by showing two similar curves for people with Hispanic origin. As for white males, the age of peak mean income increases with time.

The observed increase in the peak age in the mean income curve is a reliable feature which is accurately (in quantitative terms) explained by our model. However, there also exists the difference between mean income curves for different genders and races. For example, the mean income curve for white males peaks at higher age than the overall curve, as Figure 8 demonstrates. Figures 9 and 10 reveal the same feature in the mean income curves for male and female population, respectively, and compare three races. Figure 11 illustrates the fact that the most recent mean income trajectories of the “lagging” gender and races actually almost repeat the earlier trajectories for the “leading” gender-race configuration. All these observations are a challenge to our model predicting that the age distribution of mean income depends only on the real GDP per capita. Everything else being equal, the shape of mean income curve for white males must be similar to the shape of mean income distribution for all other gender-race configurations. Assuming the model is correct our current task is to find the model feature which does not fit reality for some reason. It is worth to identify this (-ese) reason(s) in order to understand its (their) impact on the distribution of personal income in the USA. If the impact is negative and can be controlled by socio-economic measures, one has to develop an adequate policy to improve the performance of the U.S. economy and likely society.  

Figure 6. The evolution of age-dependent mean income for white male between 1974 and 2013.  Upper panel – real mean income. Lower panel: both curves in the upper panel were normalized to their respective peak values.

Figure 7. The evolution of the age-dependent mean income for Hispanic population. 

Figure 8. The age-dependent mean income distribution for all population, male, and white male in 2011. 

Figure 9.  Comparison of the age-dependent mean income distribution in 2013 (2012 for Hispanic) for three races of male population. The white male distribution peaks at a larger age with the black and Hispanic population having similar peaks.

Figure 10.  Comparison of the age-dependent mean income distribution for three races of female population. The white male distribution peaks at a slightly larger age, but the difference with the black and Hispanic population is much smaller than for white male.

Figure 11. Comparison of mean income evolution with age for white and black male and female. Both curves for the whites lead by approximately 25 years corresponding curves for the blacks. The similarity of shapes is extraordinary, considering the lag of 25 years.

Our model is based on an assumption that any income is earned by a person with a given work capability (which is slightly different from the term “human capital”, but the latter term is adopted in the conventional economics as the productive force related to people) which is applied to some working instrument (aka work capital - the real value of all machinery, equipment, buildings, hardware, software, brands, etc.) Formally, the relationship between income, personal capability, and the size working instrument is similar to the Cobb-Douglas production function linking total production to labour and capital for the whole economy, but at the personal level. The key difference between mathematical representation of our model and the Cobb-Douglas function consists in the additional term describing all external and internal forces counteracting otherwise unlimited income growth (similar to term discounting adopted in economics). We call this process “dissipation” as adopted in physics since the rate of “discounting” is proportional to the attained level of income and inversely proportional to the size of work instrument. A good example from physics would be the evolution of average temperature in a sphere heated by homogeneously distributed internal source and cooled only through its surface. When the energy flux through the surface is proportional to its temperature, the final (stationary) temperature depends only on the sphere radius, ceteris paribus. Numerous observations confirm that the growth of personal income with age together with the income averaged over the whole population follows the same trajectory as the temperature of a sphere heated from zero.

Having the defining equation for one person one can predict the overall income evolution when all individual capabilities to earn money and all sizes of work instruments (work capital) are known. In our model, we assume that all people (independent on race and gender) are distributed evenly over their personal work capability (which ranges from 2 to 30) and the size of instrument they use to earn money (2 to 30).  So far, this assumption worked well for total population. Indeed, actual deviations from the uniform distribution related to gender and race disparity may be just marginal. When the largest part of the highest incomes belongs to white males, who are the biggest part of population with income, the deprivation of income existing in other races and gender is not seen well. For example, when 10,000 people (different from white males) reside in the middle-income range instead to progress into the highest income group the effect on the average income in both income ranges is likely too small to be seen in the overall distributions.  Since the biggest work instruments do exist but are not used by these deprived people, these instruments are then used by white males with lower human capital. This replacement makes the difference between predicted and observed incomes even smaller and the model gives an accurate prediction. 

Consequently, one explanation to the difference in the mean income curves in Figure 8 is that the distribution over work capability and/or work capital is not even. Then the difference in income distribution between genders and races can be dramatic. The purpose of this study is to demonstrate that the distribution over work capital is the same for both genders and all races, while the working capital is not distributed uniformly.

The highest incomes

At first, we would like to establish the fact that the whole female population and not-white males have severe deficit among persons with the highest incomes. Figure 12 displays the age-dependent share of white male and white female population with incomes above $100,000 as measured by the CB in 2013. To calculate these distributions we divided the population with income above $100,000 in a given age bin to all relevant (male or female) population in the same bin. As a result, the share of population is obtained for each age bin and both genders.  Figure 13 demonstrates that both curves (together with the overall curve) have the same peak age. According to our model, this means that the distribution of personal capabilities and sizes of work capital is uniform for both genders in the high-income bin. However, males are two-three times more frequent among high-income population than females.  Figure 14 presents three age-dependent ratios of male and female shares in the high-income bin for three races. Between 25 and 65 years of age, these ratios fluctuate in the range from 2 to 3. Independent on race, males are 2 to 3 times more “successful” than females, with the whites having a slightly higher ratio between 30 and 60.  

Figure 15 illustrates the advantage of white males over black and Hispanic males. The white male share in the high-income bin (above $100,000) is 2 to 3 times larger for ages between 25 and 65, as Figure 16 shows. Overall, the advantage of white male over black or Hispanic female is between 4 and 9. This disparity does not mean that females and not-white races have smaller human capital (the capability to earn money). Since the peak ages of all distributions are the same, our model suggests that the distribution over capabilities and instrument sizes was the same for all races and genders. However, in all other categories except the “white-male” one, 60% to 90% of people with the highest capabilities to earn money were deprived of well deserved highest-size working capital.

However, there is no reason to think that these people have lost their capabilities. Instead of the highest instruments (work capitals) they are forced to use some smaller instruments.  This replacement has two outcomes. Firstly, the largest instruments are now occupied by white males with slightly lower capabilities. This affects the rate of income growth for these “substitutes” and they reach the Pareto distribution slightly later than it would happen for people from the deprived gender and races with the highest capabilities. This effect is hard to reveal using the crude measurements provided by the CB. The CPS survey does not cover well the not-white-male population with the highest incomes. Moreover, we do not know the exact share of people which has to be in the Pareto distribution. Despite the difficulty to accurately measure this effect we can say that it is highly important for economic growth. People with the highest income really drive the economy (at the end of the day GDI = GDP) and the earlier entrance in the highest income group of even a fraction of a percent extra people will accelerate real economic growth.  Best people do drive the economy.

Secondly, those (not-white-male) people who were shifted to lower instruments have to reach their peak income slightly earlier. Our model describes this effect and shows that very capable people quickly reach the largest possible income for a given instrument size. This is similar to heating of a smaller sphere (working instrument) with the same bulk density of heating sources.  The time needed to reach the highest possible temperature will decrease with decreasing radius.  Overall, the gifted people should decrease the age of peak mean income. This is the effect observed in Figures 8 through 11. All female and not-white-male curves are characterized by earlier peaks. This observation is a direct indication of the uniform distribution of working capabilities among both genders and all races. We are going to model these effects quantitatively and to estimate the level of downshifting.

Summary

1.   For a given year, the dependence of mean income on age differs noticeably between genders and races.

2.   The age of peak mean income depends on gender and race and increases with increasing GDP per capita.

3.   The white male distribution has the largest age of the mean income peak.

4.   The shape of the age-dependent mean income curve for white females and all other gender/race configurations repeats the shape of the white-male curve observed 20 to 30 years before.

5.   The shape of the overall mean income dependence on age is closer to that the white-male-curve since white males has the largest part of the total income and thus contributes much to the mean income figures.

6.   Our model explains all observed features by one cause – the female population and not-white races have the same distribution of the capability to earn money and consistently low sizes of work instruments (work capital) compared to those for white men.

7.   Considering the same capability to earn money for white females and other races, one can conclude that they are shifted to relatively lower work capitals by force.

8.   Equal (fair) distribution of income between genders and races has not been achieved yet.

9.   The relatively lower instrument sizes given to white females and other races make their representation in the income bins above the Pareto threshold to be lower than it must be.

10.           In turn, this effect lowers the mean income for the same age since a relatively lower numbers of rich people occur in all age groups.

11.           The faster income growth and the earlier age peak in the Pareto distribution for white females and other races indicates that their higher capacities were applied to smaller instruments (capital) in line with the deprivation of higher instrument sizes of the female population. 

Figure 12. The age-dependent share of white male and female with incomes above $100,000 in 2013. The distribution of female population is not well measured due to insufficient representation of high-income females in the ASEC survey.

 

Figure 13. The age-dependent share of white male and female population with incomes above $100,000 in 2013, both are normalized to their respective maxima. Both curves have peaks at the same age as well as the overall (“All”) curve.

Figure 14. The ratio of male and female high-income distributions for three races. Between 25 and 65 years of age, these ratios fluctuate in the range from 2 to 3. 

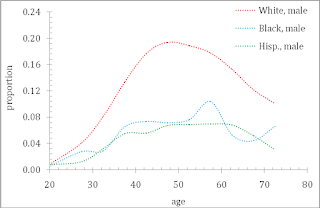
Figure 15. The age-dependent share of white male, black male and Hispanic male population with incomes above $100,000 in 2013. The distribution of black and Hispanic population is not well measured due to insufficient representation in the high-income bin in the ASEC survey.

Figure 16. White/black and white/Hispanic ratios for the high-income male population. Between 25 and 65 years of age, these ratios fluctuate in the range from 2 to 3. 

Some policy recommendations

As a principal result of this study, we propose to develop a responsible social policy aimed at the acceleration of real economic growth. Equal opportunity for genders and races to use the largest instruments of working capital will bring immediate increase in real Gross Domestic Income, i.e. in Gross Domestic Product. The effect of this social policy will be also observed in the long-run, before the distribution of instrument sizes over genders and race becomes even. Here we do not even say about the resulting social equality which will be the outcome of income equality between races and genders. This does not imply income equality between people, however.