Predicting stock prices: General Electric Company to hold

It’s time to model the stock price evolution of General Electric Company (NYSE: GE). GE is a company from Industrial Goods sector which “operates as an infrastructure and financial services company worldwide”. Among others, the studied company has a Transportation segment covering a wide range of services. This is important for understanding of the model. 

All models have been obtained using our concept of stock pricing as a decomposition of a share price into a weighted sum of two consumer price indices (CPIs). The background idea is a simplistic one: there is a potential trade-off between a given share price and goods and services the company produces and/or provides. For example, the energy consumer price should influence the price of energy companies. Let's assume that some set of consumer prices (as expressed by consumer price index, CPI) drives the company stock price, i.e. the change in the consumer prices is directly transferred into the relevant stock share price. The net effect of the CPI change can be positive or negative. The latter case implies that the rising consumer prices suppress the stock price.  

 

In real world, each company competes not only with those producing similar goods and services, but also with all other companies on the market. Therefore, the influence of the driving CPI on the company's stock price should also depend on all other CPIs. To take into account the net change in the whole variety of market prices, we introduce just one reference CPI best representing the overall dynamics of the changing price environment. Hence, the pricing model has to include at least two defining CPIs: the driver and the reference. Because of possible time delays between action and reaction (the time needed for any price changes to pass through), the defining CPIs may lead the modeled price or lag behind by a few months. 

We have borrowed the time series of monthly closing prices (through March 2014) of GE from Yahoo.com and the relevant (seasonally not adjusted) CPI estimates through February 2014 are published by the BLS.  The evolution of GE share price is defined by the index of transportation services (TS) and the index of pets, pet products and services (PETS). These indices are selected by LSQ procedure (see Appendix) from a large set of 92 CPIs covering all categories. All possible pairs of CPIs with all possible time lags and leads (but less than 12 months) were tested one by one and the set minimizing the model error is considered as the defining one. For GE, the defining time lags are 6 and 2 months, respectively, and the best-fit model is as follows:  

GE(t) =  -1.536PETS(t-2) – 0.631TS(t-6)  + 11.805(t-2000) + 291.08,  February 2014 

where GE(t) is the GE share price in U.S. dollars,  t is calendar time. All coefficients were estimated using linear regression together with their unceratinties. Table 1 confirms that all coefficients are statistically significant. In addition, the predicted and observed time series are cointegrated, i.e. the estimate of the coefficient of determination R²=0.93 is not biased. 

Table 1. Statistical estimates for the model coefficients

	Coefficients	Standard Error	t Stat	P-value	Lower 95%	Upper 95%
d	291.08	10.5133	27.670	6.72E-55	270.095	311.7124
b1	-1.536	0.0439	-34.972	4.42E-66	-1.62381	-1.44985
b2	-0.632	0.0512	-12.325	2.79E-23	-0.73194	-0.52938
c	11.805	0.4211	28.024	1.73E-55	10.96724	12.63418

Figure 1 displays the evolution of both defining indices since 2003.  Figure 2 depicts the high and low monthly prices for GE share together with the predicted and measured monthly closing prices (adjusted for dividends and splits). 

Why does the index of pets, pet products and service in the above model “define” the evolution of GE price? Actually, the model implies that PETS index does NOT affect the share price. This index provides a dynamic reference rather than the driving force. Here is a simple example how to understand the term "dynamic reference". Imagine that a swimmer needs to swim 20 km along a river. Let's assume that for this experienced swimmer the average speed is 5 km/h. How much time does s/he need? The quick answer 4 hours is wrong. One cannot calculate the time needed without knowing the (river) stream speed and its direction. This stream is the dynamic reference (or moving coordinate reference system) for the swimmer. The stream speed can also vary over time producing a non-stationary coordinate reference system. Same is with stock prices - knowing the driving CPI is not enough to calculate the price change, one needs to know "the stream speed" or the market movements. The CPI representing the dynamic reference for GE (PETS) is selected from the full set of 90+ CPIs to minimize the LSQ model residual. There is no other interpretation of this reference CPI except the statistical one.   

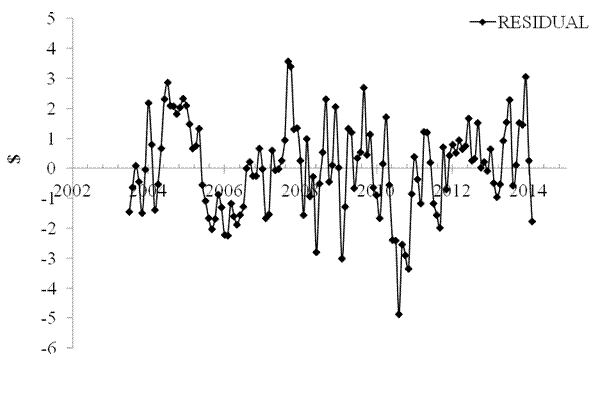
The model is stable over time. Table 2 lists the best fit models, i.e. coefficients, b1 and b2, defining CPIs, time lags, the slope of time trend, c, and the free term, d, for 7 months. The same model was obtained in 2012, 2011, and 2010 as listed in Table 2. Therefore, the estimated GE model is reliable over 50+ months.  The model residual is shown in Figure 3. The standard deviation between July 2003 and February 2014 is $1.51.  

Overall, the model does not foresee any big change in GE price any time soon, except fluctuations within the bounds of intermonth changes observed in the past. The predicted value for May 2014 is $27.7 (+-$1.5).  

Table 2. The best fit models for the period between May 2010 and February 2014

Month	b1	CPI1	lag1	b2	CPI2	lag2	c	d
Feb-14	-1.536	PETS	2	-0.632	TS	6	11.805	291.08
Jan	-1.546	PETS	2	-0.633	TS	6	11.872	292.10
Dec-13	-1.547	PETS	2	-0.634	TS	6	11.883	292.39
Nov	-1.531	PETS	2	-0.638	TS	6	11.815	291.87
Oct	-1.522	PETS	2	-0.641	TS	6	11.773	291.54
Sep	-1.513	PETS	2	-0.644	TS	6	11.732	291.24
Aug	-1.510	PETS	2	-0.645	TS	6	11.723	291.16
Jul	-1.512	PETS	2	-0.644	TS	6	11.728	291.14
Nov-12	-1.549	PETS	2	-0.711	TS	6	12.275	307.94
Oct	-1.544	PETS	2	-0.712	TS	6	12.250	307.75
Sep	-1.540	PETS	2	-0.714	TS	6	12.235	307.77
Aug	-1.530	PETS	2	-0.719	TS	6	12.198	307.95
Jul	-1.527	PETS	2	-0.720	TS	6	12.175	307.78
Jun	-1.522	PETS	2	-0.723	TS	6	12.165	308.06
May	-1.513	PETS	2	-0.732	TS	6	12.151	308.95
Apr	-1.507	PETS	2	-0.740	TS	6	12.152	309.86
Dec-11	-1.520	PETS	2	-0.785	TS	6	12.443	196.23
Nov	-1.510	PETS	2	-0.802	TS	6	12.479	197.24
Oct	-1.506	PETS	2	-0.806	TS	6	12.475	196.70
Sep	-1.495	PETS	2	-0.830	TS	6	12.539	198.53
Aug	-1.495	PETS	2	-0.828	TS	6	12.528	197.20
Jul	-1.499	PETS	2	-0.831	TS	6	12.566	196.60
Jun	-1.494	PETS	2	-0.830	TS	6	12.535	195.46
May	-1.486	PETS	2	-0.846	TS	6	12.572	196.39
Dec-10	-1.450	PETS	2	-1.006	TS	6	13.153	226.64
Nov	-1.427	PETS	2	-1.040	TS	6	13.200	229.69
Oct	-1.435	PETS	2	-1.027	TS	6	13.180	227.00
Sep	-1.442	PETS	2	-1.016	TS	6	13.165	224.57
Aug	-1.447	PETS	2	-1.006	TS	6	13.147	222.22
Jul	-1.487	PETS	2	-0.949	TS	6	13.097	214.03
Jun	-1.500	PETS	2	-0.925	TS	6	13.056	209.88
May	-1.515	PETS	2	-0.899	TS	6	13.017	205.42

 

Figure 1. The evolution of TS and PETS indices 

Figure 2. Observed and predicted GE share prices.

Figure 3. The model residual error: stdev=$1.51. 

Appendix

The concept of share pricing based on the link between consumer and stock prices has been under development since 2008. In the very beginning, we found a statistically reliable relationship between ConocoPhillips’ stock price and the difference between the core and headline consumer price index (CPI) in the United States. Then we extended the pool of defining CPIs to 92 and estimated quantitative models for all companies from the S&P 500. The extended model described the evolution of a share price as a weighted sum of two individual consumer price indices selected from this large set of CPIs. We allow only two defining CPIs, which may lead the modeled share price or lag behind it. The intuition behind the lags is that some companies are price setters and some are price takers. The former should influence the relevant CPIs, which include goods and services these companies produce. The latter lag behind the prices of goods and services they are associated with. In order to calibrate the model relative to the starting levels of the involved indices and to compensate sustainable time trends (some indices are subject to secular rise or fall) we introduced a linear time trend and constant term. In its general form, the pricing model is as follows:

sp(t_j) = Σb_i∙CPI_i(t_j-t_i) + c∙(t_j-2000 ) + d + e_j                         (1)             

where sp(t_j) is the share price at discrete (calendar) times t_j, j=1,…,J; CPI_i(t_j-t_i) is the i-th component of the CPI with the time lag t_i, i=1,..,I (I=2 in all our models); b_i, c and d  are empirical coefficients of the linear and constant term; e_j is the residual error,  whose statistical properties have to be scrutinized. 

By definition, the bets-fit model minimizes the RMS residual error. It is a fundamental feature of the model that the lags may be both negative and positive. In this study, we limit the largest lag to eleven months. System (1) contains J equations for I+2 coefficients. We start our model in July 2003 and the share price time series has more than 100 points. To resolve the system, standard methods of matrix inversion are used.  A model is considered as a reliable one when the defining CPIs are the same during the previous eight months. This number and the diversity of CPI subcategories are both crucial parameter.