How the U.S. Census Bureau fakes population data

Selected results of the 2010 census are available now. We first analyze the age pyramid. In a series of papers we have shown that the evolution of age distribution, i.e. the rate of change of some specific age, defines the rate of real economic growth [1, 2], the rate of participation labor force [3], labor productivity [4], the S&P 500 returns [5], and the level of income inequality [6]. Therefore, the page pyramid has to be measured precisely.  

In the past, we found several weird features. One of them is the deviation between the postcensal and intercensal population estimates. The latter take the advantage of decennial censuses and redistribute the so called error of the closure (the difference between estimated population and that enumerated in decennial censuses) over the previous decade. The postcensal estimates are progressively built from the reference censuses by adding net migration, birth and deaths as taken from various administrative and statistical sources.

The Census Bureau has also to retain the differences between adjacent age cohorts (one year of age) intact.  Obviously, the relative distribution over ages (the share of a given age) has to be taken from censuses (where else) and then extended in the postcensal population estimates.  The evolution of the number of people with a given age is defined by many factors, but the difference with an adjacent cohort should not significantly change over time. All these factors (e.g. migration and death rate) do not differ much for neighboring ages.   

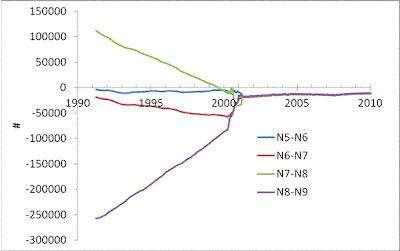
Figure 1 shows an example of the difference between several adjacent cohorts and the artificiality of the Census Bureau’s approach. The difference between the number of five-year-olds (N5) and six-years old (N6) one year after (N5 are those who are the biggest part of the six-year-olds a year after) was very small before 2001 and is small after 2001. The difference between N7 and N8 was evenly redistributed between 1991 and 2000. Then in 2001 we observe a strange rectangular valley which ends up in the same difference after 2001 as the N5-N6 difference. Since N7-N8 is positive the number of seven-year-olds exceeds the number of eight-year-olds in one year by 100,000 to 50,000. This is highly suspicious result. The measurement accuracy of the defining age of nine years shows even a worse performance. The difference is evenly distributed between 1991 and 2000. Then a sharp step of 75,000 people in 2001 ends in the same behavior after 2001 as observed for all differences. The yearly population increment (e.g. N5-N6) should depend on age and year, but the Census Bureau has fixed it over ages and time. This is more than weird.

We have to conclude that distribution of the single year of age populations are highly biased by the Census Bureau before and after the 2000 census. This introduces a significant disturbance in the statistical estimates of the link between real GDP and age pyramid.  

Figure 2 depicts the difference between the 2010 census estimates (April 2010) and the postcensal estimates for the same month as a function of age. This is the closure error. One can conclude that the postcensal estimates of the younger population were poor. Unfortunately, the intercensal estimates with the 2010 census data will likely be biased as well.

Figure 1. The differences between populations of adjacent ages where the older population is taken one year later (e.g. N5(May 1995)-N6(May 1996)).

Figure 2. The difference between the population enumerated in the 2010 census (April 2010) and the postcensal estimates for April 2010 as a function of age.