In May 2011, we presented 1000 arguments against the Solow growth model, which states that the rate of change in real GDP per capita must approach some constant level. Here we present new arguments against the Solow model as based on the historical GDP data developed by Angus Maddison at the Groningen Growth and Development Centre. In two previous posts we presented the cases of USA and Austria. We showed that the annual increment of GDP per capita is constant from 1871 to 2010 with an artificial structural break between 1940 and 1950. In other words, the slope of linear trend in real GDP per capita and thus the mean annual increment jumped by a factor of 10 between 1940 and 1950. Here we summarize numerous observations for the developed counties presented in the May’s post and validate our model.
Under our empirical framework [1,2,3], real GDP per capita in developed countries grows as a linear function of time, we call it inertial growth, when population pyramid does not change much in the long run:
G(t) = At + C (1)
Relationship (1) defines the linear trajectory of the GDP per capita, where C=Gi(t0)=G(t0) and t0 is the starting time. In the regime of inertial growth, the real GDP per capita increases by the constant value A per time unit. The relative rate of growth along the inertial linear growth trend, g(t), is the reciprocal function of G:
Relationship (2) implies that the rate of GDP growth will be asymptotically approaching zero, but the annual increment A will always be constant. This is different from the Solow model where the rate of growth is a positive (nonzero) value. Moreover, the absolute rate of GDP growth is constant and is equal to A [$/y]. This constant annual increment thus defines the constant “speed” of economic growth in a one-to-one analogy with Newton’s first law. Hence, one can consider the property of constant speed of real economic growth as “inertia of economic growth” or simply “inertia”.
In Figure 1 (borrowed from the post in May 2011), we present annual increments of real GDP per capita (borrowed from the Conference Board Total Economic database, TEDI) in the biggest developed economies as a function of real GDP per capita in sense of equation (1). These plots validate our empirical finding and reject the Solow model. Overall, there were 19 countries analyzed in the study and no one has any distinct positive trend over the past 60 years, i.e. between 1950 and 2010. So, we had 1000 years supporting the hypothesis of a constant (but country dependent) annual increment.
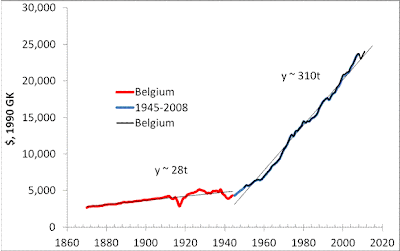
Figure 2 extends all time series back to 1871 by using the Maddison’s historical estimates of real GDP and population in developed courtiers. All estimates are in 1990 International Geary-Khamis dollars which allow a cross-country comparison. These dollars are different from 2010 EKS dollars in Figure 1. Thus the mean values may not coincide between these Figures. We have also plotted the estimates of real GDP per capita from the Total Economic Database (TEDI) now available through 2011. Essentially, this is the same data set as in the historical database and all curves after 1950 have to coincide, but Japan and Spain show significant discrepancy during the most recent period. For Japan, the TEDI and historical curve started to deviate in 1993.
Overall the time series before 1940 and after 1950 are both well approximated by linear time trends with slopes suddenly increasing by approximately a factor of 10. Not considering the reasons for this break in the tie series we just conclude that the annual increment is constant before 1940 and after 1950, as stated by our model of real GDP growth. This validates our model and rejects the possibility for the Solow model to be right.
There are important implications of the constant annual increment for economic policy in developed countries. Economists and economic authorities (like FRB and CBO) are waiting for a significant increase in the rate of real economic growth to close so called output gap, i.e. the difference between the measured level of real GDP and that expected form exponential extrapolation of the trend observed before 2007. In reality, there is not output gap, as Figure 1 and 2 demonstrate. Only Italy and Japan are far below the linear trend in real GDP per capita and Australia is above the expected level. France is also slightly below its long term linear trend. These countries might expect a recovery to the trend in the long run, depending on the evolution of their age pyramids.
The US and UK have been returning to the trend during the recent crisis and should not wait for any elevated rate of real economic growth. The expectation of a growth rate of 3.5% per year (in terms of GDP per capita) which has been explicitly articulated by the FRB and CBO in their economic outlooks is a naïve extrapolation of exponential growth related to the exponential population growth.
Figure 1. Dependence of annual GDP increment on GDP (both real per capita) for select developed countries. Original GDP data are extended by those corrected for the ratio of total and working age population (the latter must be used in GDP per capita calculations). For both time series linear regression lines and equations are shown with corresponding slopes. For the biggest countries these slopes are very close to zero but can be positive or negative. A zero slope corresponds to constant annual increment.
Figure 2. The evolution of real GDP per capita in developed countries between 1871 and 2011.























No comments:
Post a Comment