HPQ share price. December 2010 revision

Half a year ago we presented a model of the evolution of HPQ share price. We decomposed it into two CPIs, linear time trend and constant. It’s good time to revisit the prediction and the model.

According to [1], the model for Hewlett-Packard (HPQ) is defined by the index of food and beverages (F) and that of rent of primary residency (RPR). The former CPI component leads the share price by 4 months and the latter one leads by 5 months (i.e. one can predict at a four-month horizon). Figure 1 depicts the overall evolution of both involved indices. These two defining components provide the best fit model between November 2009 and December 2010. One coefficients is negative and one is positive together with time trend, with slope of 1.34.

So, the best-fit 2-C model for HPQ(t) share price is as follows:

HPQ(t) = -3.45F(t-4) +3.38RPR(t-5) + 1.34(t-2000) – 69.3

This model is slightly different from that in the previous post on HPQ. The index of food has replaced that of food less beverages (FB). The difference between these indices is practically negligible, however. Both coefficients are practically the same as before. Hence, the model has not changed in practical terms.

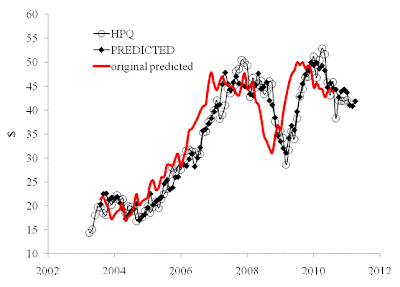
The predicted curve in Figure 2 leads the observed price by 4 months with the residual error of $2.39 for the period between March 2003 and December 2010. One can consider the price of a HPQ share as completely defined by the behaviour of the two CPI components.

The model does predict the share price in the past and foresaw the fall in 2010 four months in advance. The HPQ price is not expected to change in the first quarter of 2011.

Figure 1. Evolution of the price of F and RPR.

Figure 2. Observed and predicted HPQ share prices. The contemporaneous prediction is shown by red line. Black diamonds present the original line shifted 4 months ahead, i.e. the model.

Figure 3. Residual error of the model. Mean residual error is 0 with standard deviation of $2.29. The largest error was observed in July 2010 (-$6.31).

References

1. Kitov, I. (2010). Deterministic mechanics of pricing. Saarbrucken, Germany, LAP Lambert Academic Publishing.