We
have already mentioned that Japan is the best illustration of our concept linking inflation/unemployment
to the change in labour force. In our previous
post on the GDP deflator in Japan in 2011, we showed two cumulative curves for
observed and predicted inflation since 1980. Here we add two more readings in
both curves and conclude that our concept is quantitatively excellent. It gives
an extremely accurate long term equilibrium relation between the GDP deflator, DGDP, and labour force. The underlying data have been borrowed from the OECD and Japan Statistics.
The most important message for Japan is that
the overall level of prices associated with GDP is back to 1980 and the long
term fall will continue into the next few decades.
By trial-and-error, we seek for the
best-fit coefficients in the linear and lagged link between inflation and labour
force. Because of the structural (measurement related) break in the 1980s, we
have chosen the period after 1981 for linear regression, which is common for
almost all economic studies related to Japan. By varying the lag and coefficients
we have found the following relationship:
p(t) = 1.9dLF(t-t0)/LF(t-t0) – 0.0084 (1)
where the time lag t0=0 years; Figure 1 depicts
this best-fit case. There is no time lag between the inflation series and the
labour force change series in Japan. Free term in (1), defining the level of price
inflation in the absence of labour force change, is close to zero but negative.
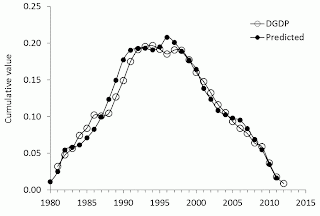
A more precise and reliable representation
of the observed and predicted inflation consists in the comparison of
cumulative curves shown in the lower panel of Figure 1. We always stress that
the cumulative values of price inflation and the change in labour force are the
levels of price and labour force, respectively. Therefore, the summation of the
annual reading gives the original estimates of price and workforce, which when are
converted into rates.
Another advantage of the cumulative
curves is that all short-term oscillations and uncorrelated noise in data as induced
by inaccurate measurements and the inevitable bias in all definitions are
effectively smoothed out. Any actual deviation between these two cumulative
curves persists in time if measured values are not matched by the defining
relationship. The predicted cumulative values are very sensitive to free term
in (1).
For Japan, the DGDP cumulative curves
are characterized by very complex and unusual for economics shapes. There was a
period of intensive inflation growth and a long deflationary period. The labour
force change, defining the predicted inflation curve, follows all the turns in
the measured cumulative inflation with the coefficient of determination R2=0.97 (R2=0.77
for the annual estimates). (Again, these are actually measured curves.) With
shrinking population, and thus, labour force, the GDP deflator will be falling
through 2050 and likely beyond.
Figure
1. Measured GDP deflator and that predicted from the change rate of labour
force in Japan. Upper panel: Annual curves smoothed with MA(3). Lower panel: Cumulative curves between
1981 and 2012. The extremely accurate agreement between the cumulative curves
illustrates the predictive power of our model.